Todays tutorial covers How to Solve Water Equivalent Calculations to prepare you for your Second Class 2A2 exam.

The tutorial explains the concept of water equivalent and includes several practice problems in a Free PDF Download of how to derive the formula, determine the water equivalent and how to apply the calculated water equivalent to solve heat mixture calculations.

Video Tutorial: How to Solve Water Equivalent Problems (Step-By-Step)

Free PDF Download of How to Solve Water Equivalent Calculations with Practice Problems:

How to Solve Water Equivalent Calculations: Menu

• Video Tutorial: How to Solve Water Equivalent Problems (Step-By-Step):
• Free PDF Download of How to Solve Water Equivalent Calculations with Practice Problems:
• What is Water Equivalent of a Particular Mass of Substance?
• How to Derive the Water Equivalent Formula:
• Water Equivalent Formula Variables:
• Recommended Reference Material For the 2A2 Exam
• How to Solve Water Equivalent Calculations Summary:

What is Water Equivalent of a Particular Mass of Substance?

The water equivalent of a particular mass of substance is the mass m of water that would need the same quantity of heat transfer Q as that particular mass of substance to create the same temperature change DT.

When completing water equivalent calculations the exam questions will often include some type of vessel (bucket) or calorimeter (bomb calorimeter). When a substance such as water or olive oil is inside a calorimeter the temperature of the calorimeter is the same as the water or olive oil within it.

This means when the temperature of the substance within the calorimeter is altered, the temperature of the calorimeter is altered a corresponding amount. Therefore as you’ll see in the examples below it is important to consider the calorimeter as an additional mass of water equal to the calculated water equivalent of the calorimeter.

 Note: When performing these calculations (unless otherwise stated) during the mixing process of two substances it is assumed there is no heat transfer to the external environment.

 This means when two various substances are mixed together the transfer of heat will occur from the hotter substance to the colder substance until they reach the same resultant temperature.

 The loss of heat of the hotter substance is all at the expense of the heat absorbed by the colder substance. The increased heat of the cooler substance is at the expense of the heat lost of the hotter substance.

How to Derive the Water Equivalent Formula:

To derive the water equivalent formula we need to use the specific heat capacity formula. We know that the quantity of heat energy transferred to the substance is dependent upon the product of the following:

• The mass of the substance.
• The specific heat of the substance.
• The temperature change of the substance.

Therefore: Q (heat transfer) = mass x specific heat x temperature change

The specific heat capacity formula is commonly written in the following two ways:

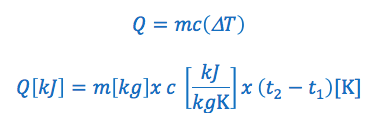
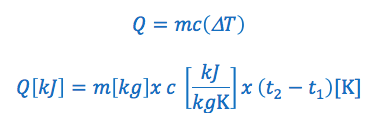
OR

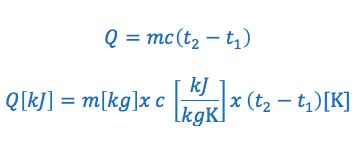
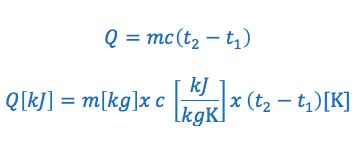
We’ll use the following example to illustrate how to derive the Water Equivalent Formula. 

Water Equivalent Formula Variables:

Q = is the quantity of heat added or removed. If it is greater then zero heat is added, if it is less then zero heat has been removed. The quantity of heat added or removed is typically expressed in kilojoules “kJ”

m = is the mass of the substance. Typically expressed in kilograms “kg”

c = is the specific heat of the substance. Typically expressed in kilojoules per kilogram per kelvin “kJ/kGK” or kilojoules per kilogram per °C “kj/kg°C”

ΔT = is the change in temperature. Typically in Kelvin or degrees Celsius for temperature.

T1 = The initial temperature of the substance. Typically in Kelvin or degrees Celsius for temperature.

T2 = The final temperature of the substance. Typically in Kelvin or degrees Celsius for temperature.

Important note: Commonly practice problems will illustrate ΔT or (T1 & T2) in degrees Celsius or Kelvin. Although the numerical values for a temperature given in Kelvin or degrees Celsius are different, ΔK or Δ°C for the two given temperatures will be the same. For example:

Recommended Reference Material For the 2A2 Exam

How to Solve Water Equivalent Calculations Summary:

Let me know your thoughts of this new format in the comments below!