How To: Determine The Thickness Of A Blank Unstayed Full-Hemispherical Head

When completing ASME code calculations involving cylindrical components it is possible during examinations you will be required to know how to determine the thickness of a blank unstayed full-hemispherical head. I recommend before working on questions involving hemispherical head questions you read over and complete the practice questions regarding How To: Determine The Thickness Of A Blank Unstayed Dished Head.

Throughout this post I will provide and formula(s) and where to find them. Describe the variables used in the formula(s). Provide insight or sketches to help describe any of the code requirements I have found particularly important for understanding blank unstayed full-hemispherical head questions. Then provide some completed practice questions to help reinforce the material before wrapping everything up with a summary of the topic.

All reference page numbers are from the 2007 ASME Boiler & Pressure Vessel Code

Formula

The formula for how to determine the thickness of a blank unstayed full-hemispherical head with pressure on the concave side is under PG-29.11 page 14.

Minimum Thickness Formula

The above equation should not be used when the required thickness of the head given by the above formula exceeds 35.6% of the inside radius, and instead these following two equations should be used:

Where

Formula Variables

The formula variables above are explained on page 14 and are as follows:

L = Is the radius to which the head was formed, measures on the concave side of the head

P = Maximum allowable working pressure

S = Maximum allowable working stress, using values given in Table 1A of Section II, Part D

t = Minimum thickness of head

w = weld joint strength reduction factor per PG-26

Important Full-Hemispherical Head Code Requirements

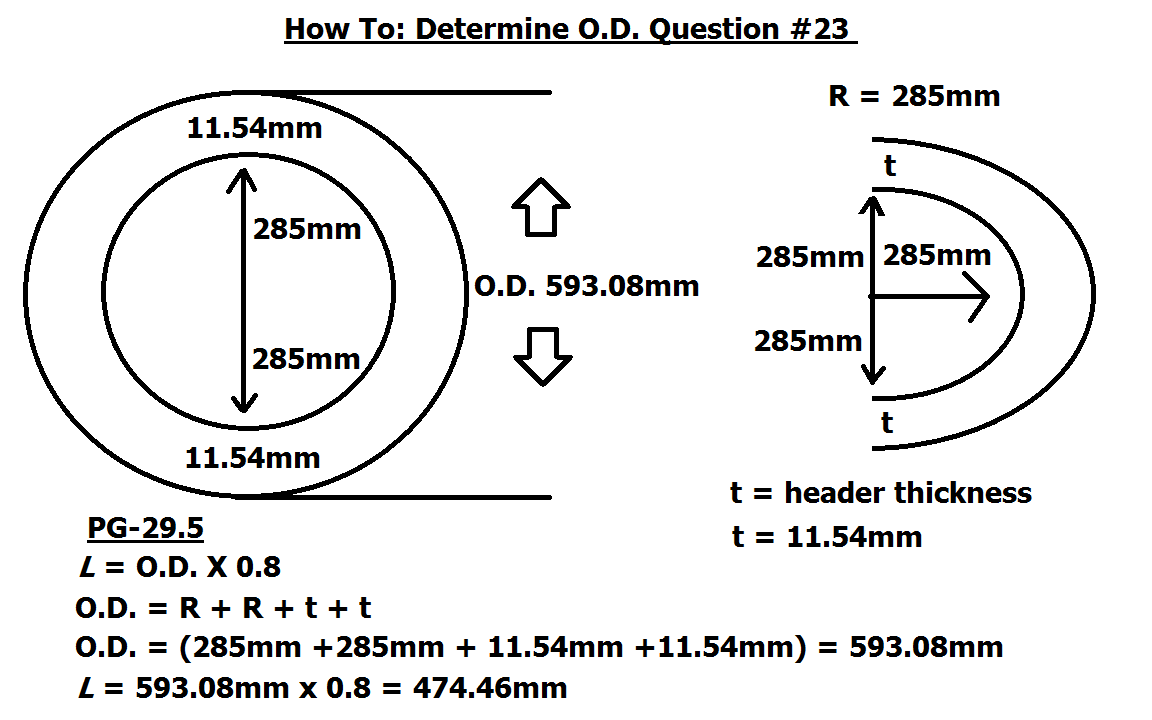
PG-29.12 page 14 – If a flanged-in manhole that meets the code requirements is placed in a full-hemispherical head, the thickness of the head shall be the same as for a head dished to a segment of a sphere ( see PG-29.1 and PG -29.5), with a dish radius equal to eight tenths the diameter of the shell and with the added thickness for the manhole as specified in PG-29.3.

[table id=1 /]